Algebraic Expressions and Polypad

I tried this activity in Heather Lyon's MTH1W class using Polypad on Mathigon to help illustrate algebraic expressions. First Q: if this is x + 2 what would 3(x+2) look like? Students go to the VNPS to work in small groups:

Some puzzled looks at first but once they began sketching what it might look like, the students saw what was happening:

I could then easily use Polypad to confirm this:

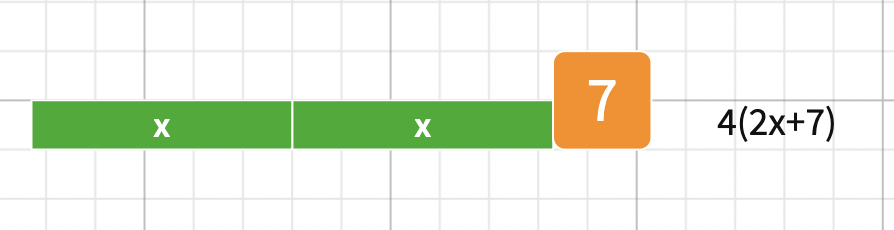
I followed this up with 5(x+4) and we could now talk of more efficient ways of drawing our thinking. All the while I'm nudging them to the array model:

Now, I want to chunk the ones so give this question. Students' array models are now becoming more efficient:

We do this for a few more example. As they are feeling confident, I want to push them so ask them to sketch out what x(2x+3) would look like. Though they have never seen this sort of question before, they connect it to the model that they have just been using:

I can quickly confirm this on Polypad:

Some students choose to use the concrete algebra tiles but I can then show them how this connects to the diagrammatic model. One of these students says 'Now I see it... and that will save time!'

A few more examples follow and while I help a couple of groups, I give an extension to others: the answer is 18x^2-27 x... what is the question? They factor this successfully without any help from me:

They have been working hard so we take a little break and I perform a little mathmagic: think of a number... add 5, double it... add 8... half it... take away the number you first thought of. By using a little chicanery with a pack of cars, I show them the nine of hearts... the number they were all left with!! I then show how I used algebra to 'rig the system'!

With a little bit of time left, we decide to see if they can use this new knowledge to solve equations. I scroll to the top of my polypad to create an equation from the first two expressions we created:

And with no fuss whatsoever, they successfully solve it!

I was thinking how this approach differed to the one I would have used when I began teaching. Then, I would have given ten examples, no visuals, all symbolic and got the students to do more exercises. Now the students (thanks to Mathigon!) are doing the math!

The link to the polypad I used is here.

A Nice Algebra Puzzle

Last week I went into a Grade 9 class that had just begun to learn about simplifying polynomials by collecting like terms. I had an idea for a task that I thought would help them with this so began by showing them this pyramid.

I explained that the numbers in two adjacent squares add to give the number in the square directly above them. With this information, I split them into visibly random groups of 3 and had them work at whiteboards to find four numbers that go in the bottom row that would give 54 in the top square.

After completing this, I then gave them this pyramid:

I wanted to see how comfortable they were with collecting like terms before giving them something more thought-provoking. Some were able to complete this symbolically and others were happy to use algebra tiles to help their thinking:

I then gave them this task:

By now, I could hear how adept the students were at collecting like terms and was impressed at the different ways they went about solving the task:

Next, I gave them this task with the restriction that all the terms on the bottom row had to be different:

Again, I was really pleased how they went about solving this (some symbolically, some using algebra tiles again) and by listening to the students talk, I could tell that they were really understanding this. I even overheard a few groups say how much fun the task was!

As this had taken less time than I expected, I had to then think quick and come up with an extension. I asked them that if the value of the top brick was 57, what would the value of the four bottom bricks be?

This required a bit of clarification for two or three groups, but once they understood it, it allowed them to demonstrate their algebraic skills in solving equations and substitution:

It was great to see all the different solutions as well as see that in some cases, the different terms actually resulted in the same value once the substitution was made.

I finished by asking them to figure out:

a) the side lengths of an isosceles triangle, given that the perimeter is 120 cm and that the two equal sides are double the size of the other other side

b) the dimensions of a rectangle given that the perimeter is 1000 cm and that the length is triple the width.

For the first problem, they did this by trial and improvement, so I walked them through how to set this up algebraically. I was pleased to see them al use this approach for the rectangle problem.

I was really happy with the way they remained engaged throughout these tasks, especially as it was a Friday afternoon and would definitely use these again.