I've been lucky enough to work with a teacher of a Grade 10 Applied class and we have been trying to adopt a more visual approach to help students make sense of solving linear systems. We began by challenging students with this puzzle:
The students worked in groups of three on vertical whiteboards and they did a pretty good job of solving this by mainly using a guess-and-check approach. It was interesting that most focussed on the middle two equations first. It allowed me to tell them that we would now learn some cool techniques to solve this pair of equations (i.e. b – c = 5 and b + c = 19). As there were some magnetic algebra tiles handy I then created some zero pairs and asked them what the value of each was:
Now it might seem like an obvious question, but in particular I needed to be sure that they were good with the idea that when they see 3x and -3x (six things), they combine to give 0.
I then used Polypad to show them this linear system:
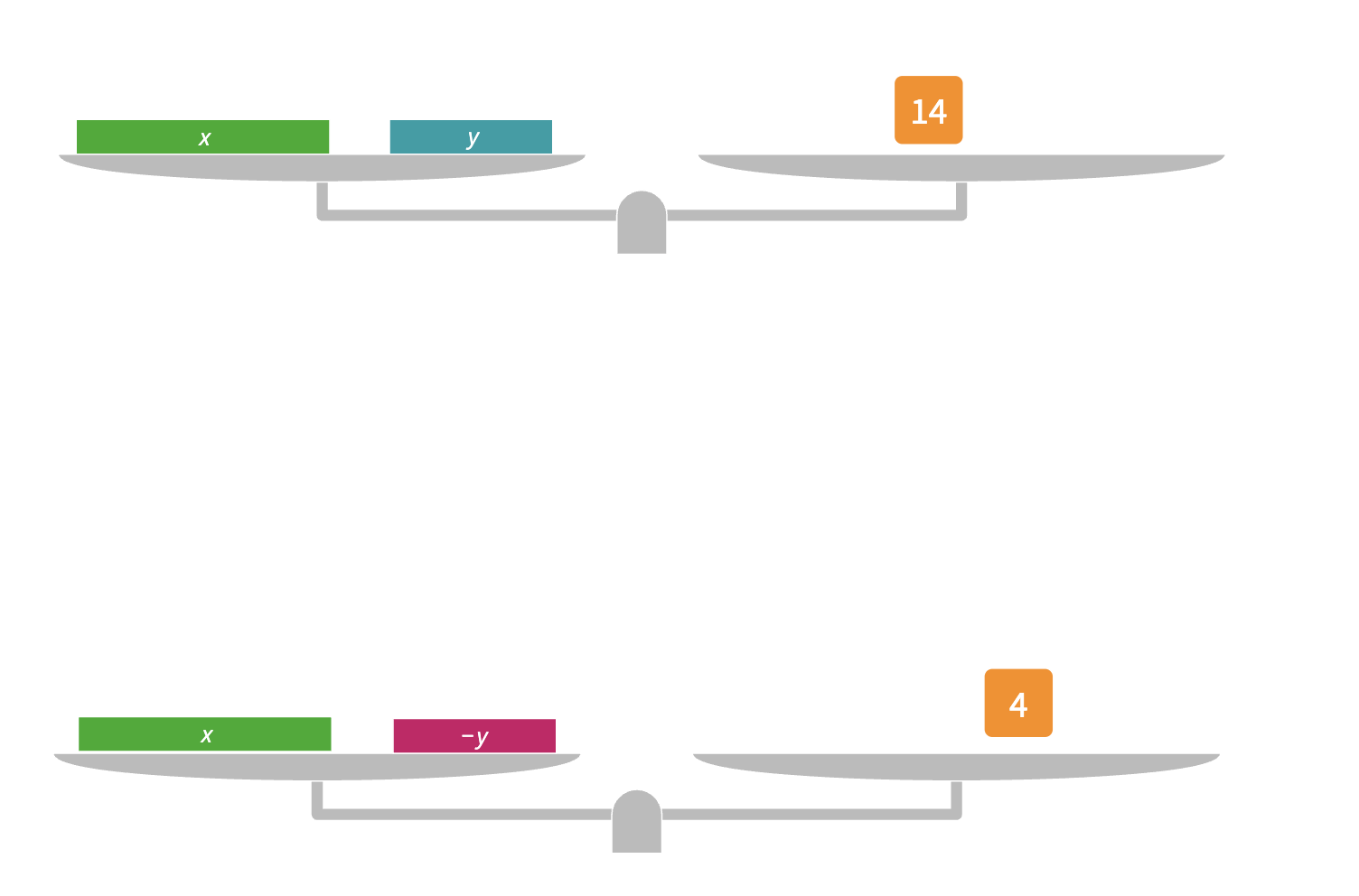
I asked them to tell me what the two equations were (i.e. x + y = 14 and x – y = 4) and then showed them how we could combine these two equations and, with the power of the zero pair, end up with a simplified equation to solve.When students saw the y and the -y bars actually be eliminated in front of their eyes, it really did seem to help them make sense of the algebra. What I like about Polypad is that I can show something visually and then alongside it write what is happening symbolically.
The students were then given other linear systems to solve in groups at the whiteboards and we were happy with what they did. Having the students work on the vertical whiteboards allowed us to move from group to group giving feedback when necessary.
This dealt with elimination when one pair of the variables are opposite quantities (e.g. 3y and -3y). But what happens when they are the same quantities (e.g. 4x and 4x)? Well, Polypad can help us again:
Finally, what happens if the linear systems do not have variables in equal or opposite amounts (e.g. 3x + 2y = 16 and x + y = 4)? Well, Polypad allows us to visualise manipulating one of these equations to create a 'match':
When the students reviewed solving linear systems by elimination, it was pleasing to see how well they did:
My thanks go to Ms. K. Perri and her wonderful class of students.
Here are the links to the various Polypads that I have created to help teach this:
