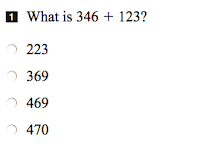A Tale of Two Questions Part 2: Junior

Continuing on from my last post, one of the things I like to do when analysing EQAO results is to look at how students responded to individual questions. Good questions that expose students' misconceptions can give us pointers as to what we can do to fine-tune our teaching.
Two questions that I found particularly interest in last year's Junior EQAO were these:

Again, when I show this to teachers, principals and parents, I ask them to predict what percentage of students they think got these correct. For the first question, bearing in mind that primary students struggled with a similar equality question, typically people reckon that about 50% of students got this correct.

The actual amount provincially is 68% and the breakdown for each response is shown below.

To an extent, this is encouraging: It would appear that students have a better understanding of the meaning of the '=' sign than their primary counterparts and chatting to a small number of junior students would at least anecdotally confirm this. From a number sense point of view, it would appear that many of them are comfortable enough to work with both a subtraction that might involve regrouping and a multiplication that requires one of the more commonly mistaken facts (i.e. 8×7=56). A very small minority (those who answered 11) appear to have added 72 and 16 instead of finding the difference. And there is another group who have answered 56. Now this maybe because they have misconceptions with the '=' sign and simply answered 72–16. But I have also seen both students and adults do something like this:

...and for whatever reason selected the 56 option in the answer key. When I saw one parent do this at one of our Math Café for parents, I asked them to tell me the value of m. They correctly told me 7. I then asked them, what answer they selected. Again they answered 7, so I asked them to look at what they had actually written. When they saw they had selected 56, they were stunned and said "How on earth did I put that?".

It made me realise that just because somebody puts the wrong answer down on a multiple choice test, doesn't mean to say that they don't understand what to do.

The second question was the answered correctly by the lowest number of junior students (34%). The actual breakdown is shown below:

It is classified as a measurement question but my sense is that the errors that are being made here are not to do with how many millilitres are in a litre. The mistakes are made because students (and adults) need to decide which operations to use. They have deficits in their operational understanding. If students are told what operation to use (e.g. calculate 45+99, work out 2496÷24) then this is computational understanding which, though useful, does not prepare them to answer the milk question. If students experience a diet of nothing but computational questions then they will always have difficulties when they have to decide what operations to use. Doing a hundred long division questions will not teach students what division is and when it should be used.

But also, if students are just given one-step word problems where they have to decide on what single operation to use, then this will not be enough to prepare them for the question above: two of the answers above are the result of students most likely selecting a single operation (6×4=24, and 250÷4=62.5≈63).

Perhaps a strategy that I would avoid at all costs is the keyword approach. Here students are taught a list of words and their accompanying operation. One of the problems with this approach is that sometimes these keywords are not present in the question (are there any keywords in the example above?). Additionally, I have seen students read a question, write down two numbers involved then an operation suggested by the keyword regardless of whether or not this makes sense:

In terms of how to develop operational understanding, my go to is always the concrete-diagrammatic-symbolic approach. It was interesting to see how adults tackled this question when I gave it to them. Some are surprised that this is on the junior EQAO as they think (rightly or not) that it is too difficult. There were more than a few who struggled to figure out what operations to use until they tried drawing a diagram: then the operations required became clearer. This is one of the reasons why I like bar models (as I have blogged before here and here.)
As operations are in essence actions, any strategy that gets students thinking about the actions involved in the question will tend to be a good one.

A Tale of Two Questions Part 1: Primary

As part of our analysis of the EQAO data form our schools, I like to move way beyond a simple percentage figure that tells how many students are at or above provincial standard. In terms of looking for data that will have an impact on the way math is taught, I find it more useful to look at how students responded to individual questions. Good questions can often expose students' misconceptions which in might in turn give us pointers as to how adapt our teaching.
Two questions which I found particularly interesting in the Primary Math EQAO were these:

Both of these questions are on the section of the paper where calculators are not allowed.

I have shared these two questions with teachers, principals, and superintendents as well as parents at the first of our Math Cafés for Parents. I ask them to do the questions and then tell me which one they think was the most difficult to do. Some think the first one is more difficult because it has large numbers, whilst others think that the second one requires a bit more thinking even though the numbers involved are small.

I then ask them to estimate what percentage of students they think got the first answer correct. Bearing in mind that my audiences have heard and read a lot about how students are not taught the basics (whatever they are) and that they are not required to learn facts (which is definitely not true) I get a range of answers from 30% to 70%. 

I then tell them that provincially 88% of our students got this correct.

This is surprising for the people I show it to and I can get them to agree that this shows us that students, in general, can add two 3-digit numbers without a calculator. Now I don't know how many of these students did this mentally, or how many needed to write the numbers in columns to use a standard algorithm, or how many used an empty number line, or whether we would have got different answers if some regrouping was required. But I do know that for this question, the vast majority of students met the expectation, contrary to how adults expected them to perform. I then ask the question: do you think that this question shows that the vast majority of our students understand addition. Most people say yes.

The second question is more interesting. Again, I ask the question: what percentage of students do you think got this question correct. Typically I get a range of answers from 20% to 60%. 

The actual provincial results are that 43% of students got this correct.

I find this statistic incredibly informative. Firstly, this is not a 'gotcha' question. It is explicitly stated in the curriculum and a version has been used on many previous EQAO tests. In fact, previous EQAO tests would have had one answer as 9 but this was not an option on this year's test as too many students were choosing it! We actually gave this question as is to all the current grade 3s in our Board and 2% of them actually added '9' as a fifth option, drew a circle alongside and helpfully shaded this in! The actual provincial breakdown for this question is as follows:

Notice that almost as many students selected the incorrect answer '12' as the correct answer. These students have just added all the numbers that they see.

But why do so few get this correct? It isn't anything to do with not knowing their addition facts as we would have seen lower marks in the first question. Instead, I think that this is due to our students not understanding what the equals sign means (as I have written about before here).

For all the talk of 'going back to basics' and memorising facts, we are in danger of being blind to some extremely important mathematical concepts, in this case, the idea of equality. We can get students to develop a solid understanding of equality through the Concrete-Diagrammatic-Symbolic approach (as referred to in an earlier post here). For example, we can begin to develop a concrete understanding through models such as this: 

However, if our students experience nothing but a diet of 2 + 3 = , 9 – 6 = , 32 + 89 =  questions, then they will not develop a true understanding of equality thus putting their future math learning in jeopardy.