Two questions which I found particularly interesting in the Primary Math EQAO were these:
Both of these questions are on the section of the paper where calculators are not allowed.
I have shared these two questions with teachers, principals, and superintendents as well as parents at the first of our Math Cafés for Parents. I ask them to do the questions and then tell me which one they think was the most difficult to do. Some think the first one is more difficult because it has large numbers, whilst others think that the second one requires a bit more thinking even though the numbers involved are small.
I then ask them to estimate what percentage of students they think got the first answer correct. Bearing in mind that my audiences have heard and read a lot about how students are not taught the basics (whatever they are) and that they are not required to learn facts (which is definitely not true) I get a range of answers from 30% to 70%.
I then tell them that provincially 88% of our students got this correct.
This is surprising for the people I show it to and I can get them to agree that this shows us that students, in general, can add two 3-digit numbers without a calculator. Now I don't know how many of these students did this mentally, or how many needed to write the numbers in columns to use a standard algorithm, or how many used an empty number line, or whether we would have got different answers if some regrouping was required. But I do know that for this question, the vast majority of students met the expectation, contrary to how adults expected them to perform. I then ask the question: do you think that this question shows that the vast majority of our students understand addition. Most people say yes.
The second question is more interesting. Again, I ask the question: what percentage of students do you think got this question correct. Typically I get a range of answers from 20% to 60%.
The actual provincial results are that 43% of students got this correct.
I find this statistic incredibly informative. Firstly, this is not a 'gotcha' question. It is explicitly stated in the curriculum and a version has been used on many previous EQAO tests. In fact, previous EQAO tests would have had one answer as 9 but this was not an option on this year's test as too many students were choosing it! We actually gave this question as is to all the current grade 3s in our Board and 2% of them actually added '9' as a fifth option, drew a circle alongside and helpfully shaded this in! The actual provincial breakdown for this question is as follows:
Notice that almost as many students selected the incorrect answer '12' as the correct answer. These students have just added all the numbers that they see.
But why do so few get this correct? It isn't anything to do with not knowing their addition facts as we would have seen lower marks in the first question. Instead, I think that this is due to our students not understanding what the equals sign means (as I have written about before here).
For all the talk of 'going back to basics' and memorising facts, we are in danger of being blind to some extremely important mathematical concepts, in this case, the idea of equality. We can get students to develop a solid understanding of equality through the Concrete-Diagrammatic-Symbolic approach (as referred to in an earlier post here). For example, we can begin to develop a concrete understanding through models such as this:
However, if our students experience nothing but a diet of 2 + 3 = , 9 – 6 = , 32 + 89 = questions, then they will not develop a true understanding of equality thus putting their future math learning in jeopardy.
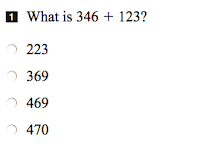



I appreciate that you have all this data, but your interpretation of the results are speculative. It might be due to "students not understanding what the equals sign means", but it might be something else. To do this properly, we should interview students and ask those who got it wrong what they were thinking.
ReplyDeleteI don't think we should ignore novelty as at least a partial explanation. Students are very good at solving problem types that they have previously solved and very bad (shockingly bad, in my experience) at solving test problem of types they have not seen before.
I teach high school math and have noticed over and over again that even a slightly novel problem type is enough to trip up huge numbers of students, even if the problem seems really easy. People are really bad at doing things correctly for the first time and really good at doing things they have done before. Concluding that students don't understand the fundamental concepts seems like an overreaction.
Many teachers will simply never test students with problems unless they have seen that exact type of problem before. I would say that this is the norm in most classrooms. Standardized test-makers frequently violate this rule, though.
I'm curious if the breakdown you outline above is simply a function of rates of exposure of the two different types of problems. My intuition is that students would easily be able to solve problems of the second type if they had done more things like that in class before. But most probably didn't.
Thanks for your comments William. Maybe it was amiss of me not to mention that I have interviewed many students who have made this mistake and they really do not know what the equals sign means. Many simply see it as 'the answer is coming up'. This is something that is not unknown to researchers. I do agree that if this is a novel problem to students then this may explain the errors. However, this type of problem is a clear expectation in the Ontario curriculum and is always on EQAO tests: students should be more than familiar with questions like this and it is up to us, as teachers, to make sure of this. Understanding this fundamental concept will put the students in a better place to develop their algebraic understanding, and, I hope, will give them more confidence when tackling novel problems.
DeleteThere is a lot research showing students conceptions related to the equal sign. For example:
ReplyDeletehttp://itp.wceruw.org/Fall%2009%20seminar/Knuthetal08.pdf
But it might also be worth thinking about the relationship between what students are experiencing in classrooms, and what our curriculum is suggesting. Take a look:
Determine, the missing number in equations involving addition and subtraction of one- and two-digit numbers, USING A VARIETY OF TOOLS AND STRATEGIES (e.g., MODELLING WITH CONCRETE MATERIALS, using guess
and check with and without the aid of a calculator)
If we want our kids to get better at math, we might want to consider just how thoughtful the writers were in creating the document!
Indeed! Having shared this question with teachers and parents, I think there is a much better awareness about the need to make sure that students are taught the true meaning of the equals sign.
Delete