Making Predictions

Here in Ontario, we have had some very cold and snowy weather recently. I took advantage of this in a Grade 5 class to see if the students could make predictions using line graphs. Getting students to predict what graphs look like is, in my opinion, as important as getting students to draw graphs from given data: it gets students reasoning, proving and reflecting.
Before going further, a little geography might be in order:

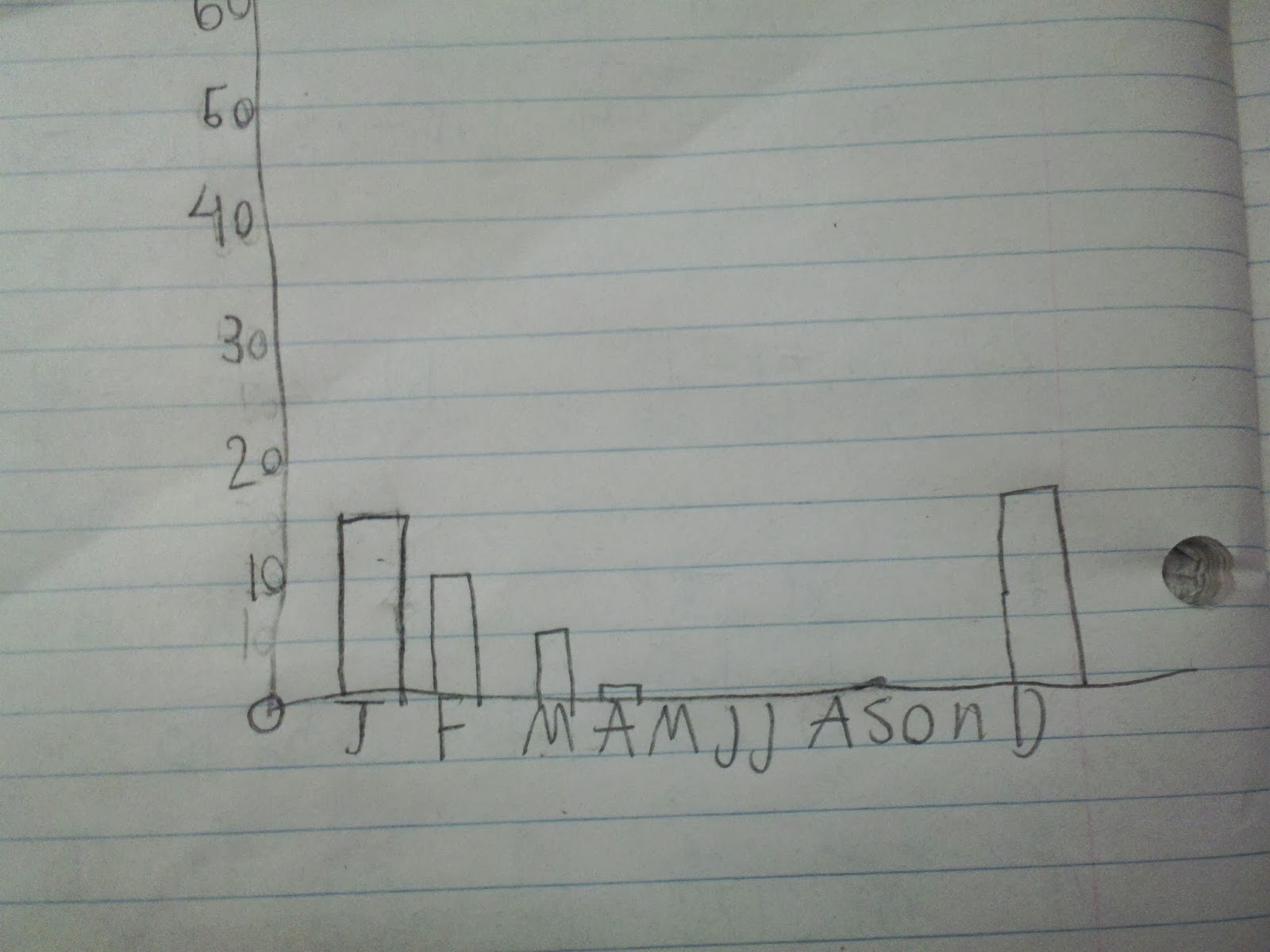
We asked students to draw a graph to predict what they thought the average snowfall per month in Toronto would be. A set of axes was drawn on the board to anchor everyone to the same scale. Initially some drew bar graphs, some vertical line graphs and some broken line graphs. As our goal was interpreting line graphs, we asked students to redraw (if necessary) their graphs so that it was a line graph. This is the sort of thing we saw:

We could then ask the students one of my favourite questions:

Look at your graphs: What is the same? What is different? 



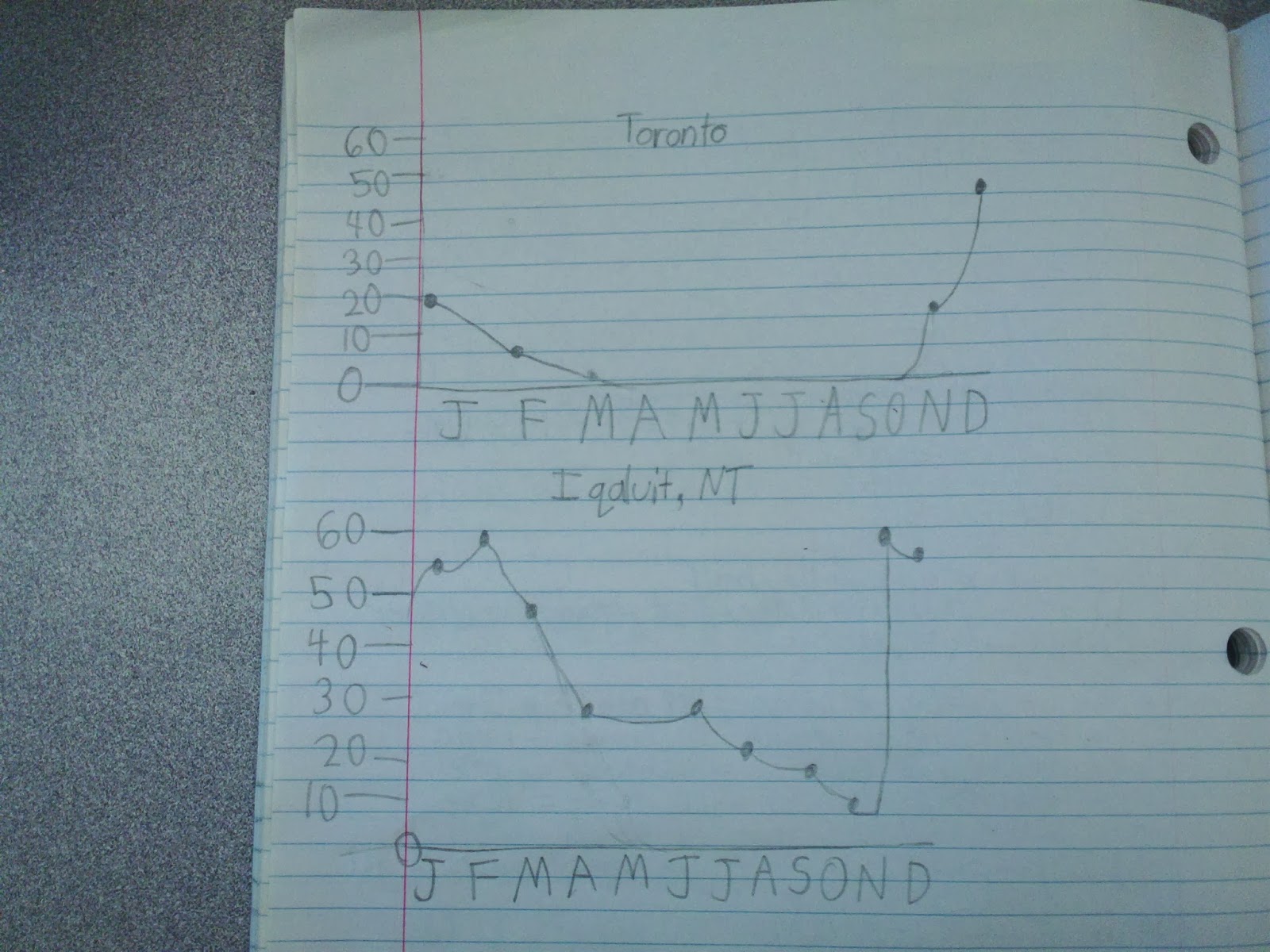
We then showed them the actual graph from  a really neat site called CityStats.ca:

There were some great conversations about how close their graphs were to the actual graph, even though they did not have access to the primary data. Also there was great discussion about the red line, what it meant and how it looks as if Toronto gets less snow than the Canadian average.
So we then asked them to predict what the graph for Iqaluit would look like (Iqaluit, the capital of Nunavut, is in the far north of Canada). What we saw was a graph similar to Toronto's but shifted upwards:

We then showed them the CityStats graph for Iqaluit...

... and it was neat to see everyone reflect that their answer was wrong (and they were OK with that) but to then think of reasons why that might be. Superimposing the two graphs we noticed a curious thing:

Iqaluit gets less snow than Toronto in the winter months!

This was a big surprise to all the students (and most of the adults). Various reasons were suggested as to why this might be until one girl said "Well in Science we've been learning about the water cycle and because it is so cold in Iqaluit, all the water will be frozen and so there will be not as much moisture in the air so there will be less snow". Now I'm not sure if this is the exact scientific reason, but it was a very impressive hypothesis!
And a lot better than my 'It's too cold to snow' excuse.

Elapsed Time Problems Using an Empty Number Line

Some time ago I gave students the question:
A movie starts at 3:40 p.m. and lasts 2 and 3/4 hours. What time will it finish?
The students (who had a very algorithmic approach to addition and subtraction) produced solutions such as: 

This particular student figuring that 5:85 is not a familiar time, decided that maybe he should have subtracted instead but then ends up with an equally bewildering 0:95!

In a previous post, I showed how the empty number line is a great tool to improve students' abilities in addition and subtraction. Today it was great to see some Grade 5 students use the empty number line to solve an elapsed time problem. The question we gave was as follows:
Mr. Huxter has a problem; he has forgotten his Grade 5 math and started cooking his turkey too late. His family couldn't eat until 8:30 p.m.! The turkey took 3 and 3/4 hours to cook. If his family wanted to eat at 6:00 p.m., what time should he have started to cook the turkey?
These students were able to decompose numbers in a variety of ways so were able to get the solution in a variety of ways:

 

One student used a mental number line to solve this and wrote his strategy thus:



We followed up the question by asking "What time did Mr. Huxter put his original turkey in?" It was again interesting to see a variety of successful approaches:  

This example below, the student starts by taking 30 minutes off to get to a friendly 8:00:

This question involved finding the start time using the end time and the elapsed time. It will be interesting to see how they solve problems when they are given the start and end times and have to find the elapsed time, or when they are given the start and elapsed time and have to find the end time. I suspect that as long as they continue to use the empty number line, they will no find these problems any more difficult.
In fact, past experience tells me that the more they use the number line, the more they will be able to visualise this and thus solve these mentally.