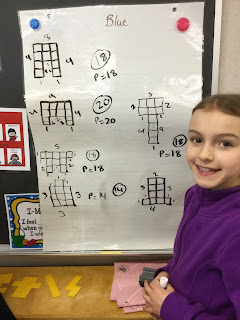Nets of Solids

One of my favourite things to teach is nets. The way I teach it is very different to the way I was taught it. Basically, I remember having to look at something like this:

and then say which of these were nets of a cube. As my spatial reasoning was net well-developed, I had trouble with this type of question. When I began teaching, I would 'teach' nets by getting students to cut out and glue something like this:

Whilst this was an improvement on how I learnt, it was all a bit messy and time-consuming. The way I teach now is much better as I get the students to use polydrons. These are two-dimensional shapes that click together to form nets that can be folded together to form a solid.

I visited two Grade 5 classes recently and, having explained what a net was, challenged the students to find as many nets of a cube as they could. The students were randomly grouped into threes and, to help them record their results, I provided one sheet of grid paper to each group.
Each group got stuck into the challenge immediately. The wonderful thing about polydrons is that it is that it is so quick for students to either prove that their net works:

 Or to disprove:

 After about ten minutes, I always get this question from students: are these two nets the same:

It is a perfect opportunity to stop the class and get their views: some say they are the same, others say that they are different. I can then tell them that to a mathematician, they are the same as they are congruent: they are exactly the same size and shape. I can even show this to the students by reflecting or rotating the nets so that they coincide.
Sooner or later, the students ask me how many nets there are so I tell them that there are eleven. If any student find this net, I make sure that they know that it is my favourite net:

 And if they find this one, I will tell them that this is the one net that I still can't believe folds to make a cube:

At the end of class, we then summarised our results: success! we had found all eleven.

 I revisited one of these classes the next day to follow up with this challenge: Find as many nets as you can of a triangular-based prism. It was fascinating to see how well the students were using their spatial reasoning to discover these nets. Again, some worked:

 And some didn't:

 Again, the students recorded their results on grid paper, taking a bit more care to draw the triangular faces:

 When students found this net, I made sure that they knew that it was my favourite:

 It was another successful lesson and at the end, I consolidated by showing all the solutions that the students found and showed them how a mathematician might classify these:

Having done all this investigation, students will now be in a better position to look at the first picture at the top of this post and use their spatial reasoning to decide which of these are nets.

Thinking Outside the 'Box'

I'm a big fan of the array or 'box' method for multiplication (as I blogged earlier here.)  A twitter chat with Britnny Schjolin last week raised this troubling point however:

I know that many of my colleagues are also impressed by it even though they, like me, might not have see it when they were students. I have also worked with colleagues who have openly stated that the 'box' method is not the proper way to show your work or that they don't like it so they won't show this to their students. I'm not sure how widespread such attitudes are but I honestly feel that we are doing our students a huge disservice by not showing them such a powerful representation that allows for so many different connections to be made. If this means that we as teachers should learn something new, then so be it: as educators we must always be prepared to learn new things.

To show how useful I have found this, here is how I recently solved a problem that I came across by using arrays or the 'box' method. 

Prove that the product of four consecutive numbers is always one less than a perfect square.

I started pretty conventionally by trying to generalise the product of four consecutive numbers:

Well, I don't fancy working out that product, but I know if I rewrite the four consecutive numbers like so:

Now I can rearrange to make use of the difference of squares to make something a little more delightful:

 A quick array is drawn to help me work out this product:

Since I have to prove that the product is one less than a perfect square then I need to consider this:

I am good at factoring quadratics by inspection but not so good with quartics! However, I now decide to draw a square array to help me factor by working out the components of each side. The first part solves itself:

To get the 2a³ term, I need to split this symmetrically across the square and think what the next component must be. This makes things very clear:

 This also helps me get the middle product:

 Now to get the -a² term, I need to have a -a² in each of the top right and bottom left cells:

This immediately gives me the last component from which I can write the term as a perfect square:

Thus the product of four consecutive numbers is always one less than a perfect square.

Now, before I learned about the array or 'box' method, I would have chugged through with the algebra and probably would have eventually reached the same conclusion. However, now I can attack and solve such problems in a fraction of the time and with more clarity. This is why we must teach this method:

It is an incredible mathematical tool.

It is not a new idea either. Recently, for fun, I have decided to work my way through Silvanus P. Thompson's classic Calculus Made Easy and I came across this:

Array models were being used back in 1910!

Open Middle Fraction Problems

I have often shared the Open Middle website as a source of good thinking problems with the teachers that I work with. This week I created a couple of my own and used them with a grade 6 class who have been working on equivalence in fractions, decimals and percentages. The first problem (given using verbal instructions) I gave was this: 

Use any of the digits 0 to 6 once only to satisfy the statement below.

We used visibly random groups to get the students into threes and gave each group seven tiles to work with. As we began to walk around the room, a few students asked 'What do I have to do?' Taking the lead from Peter Liljedahl's work, I smiled and told them to find out from a friend.

We could see some students getting stuck or making mistakes but resisted the urge to jump in and show them how to get a solution. 

We let them think their way out of it.

Sure enough, we soon heard some 'A-ha's around the room as students realised that the first space had to be a zero, and as they figured out the decimal equivalent of a fraction:

Once they had found one solution, I asked them to find me another. Some used two-fourths as the fraction, others used one-fifth or two-fifths:

One group bent the rules a little bit:

Another group tried something similar but put 2.5 instead of 0.25. I simply pointed to this and asked 'Is this more than one or less than one?' and walked away. When I came back, they had corrected it.

Another group tried this:

When I asked about this, they knew that two-sixths was one-third but they also thought that its decimal equivalent was exactly 0.3. As they knew how to use a calculator to change a fraction into a decimal, I asked them to do this for one-third. This made it easier for me to convince them that 0.3 is different to 0.333333333... 

As we had fifteen minutes left, I gave a variation of a question that I tweeted last week that proved popular:

Any thoughts we might have had about this question being tricky for them were soon dispelled:

As we circulated, we could hear the students justify their solutions and, if we were unsure, simply asked a question like "Can you convince me that two-sixths is less than five-eighths?"

One student asked if it was OK to use a fraction whose numerator was larger than its denominator. This led into a nice discussion about improper fractions and how these are all larger than one:

We could see a couple of groups who found solutions quite quickly so we gave them an added challenge by removing the '1' tile. They relished the added level of difficulty:

All in all, it was a really pleasing lesson that allowed the students to show us their problem solving skills as well as allow us as teachers to assess their understanding of fractional equivalence.

Creating Thinking Classrooms (3)

Having done some work on creating a thinking classroom with junior and intermediate students (see my last two posts), I was keen to see how high school students would react. Again, I wanted to gauge the impact of three of the optimal practices for creating a thinking classroom as outlined by Peter Liljedahl:

• start with good questions
• use vertical non-permanent surfaces
• use visible random groups of three

The first problem I tried this with was actually one Peter Liljedahl had shared with us at the Ontario Mathematics Coordinators Association's conference.
Using the numbers 1 to 10, and the operations +, –, ✕, ÷ plus another one of these operations, create five number sentences that have the following solutions:

17     2     21     3      2

(For what it is worth, this question is a lot easier to understand when the instructions are given orally!)

The students got stuck into this problem immediately. Being free to move around the room I was able to listen to some impressive number sense and logic. I'd go so far as to say that the students were more accomplished at this than adults who I have given the task to.

When they solved it, I gave another set of answers:
2    2    2    2    9
and later
10   14   1   20   16

 Next, I gave one of the Problems of the Week from our @DCDSBMath twitter feed:

As students quickly solved this, I then asked them to consider a 10-by-10 array with the top square missing and, from there, to consider the general case:

 Many groups looked at of squares of different sizes and noticed that these were one less than a perfect square. It was a nice opportunity for me to introduce sigma notation:

One group gave me math bumps though as they saw the number of squares of different sizes in a different way which connected beautifully to the difference of squares:

Perhaps the strongest feeling I take away from this is the amount of math that the students are doing. They are not sitting passively copying a note, they are actually being mathematicians.
It is something I have seen before in a Grade 9 class (this post) and I also saw recently in a Grade 12 calculus class. Students were asked to sketch a graph of any function they wanted and to then use what they know of the derivative to sketch the graph of the derivative (without resorting to deriving by first principles). Students were first sorted visibly into random groups by being given a card and then having to find the corresponding representations:

They then got stuck into the task:

 and as they did so, they began to challenge themselves more:

Remember, the students had to choose their own graphs for this activity. The discussions that took place were a joy to behold. Independently, they began to hypothesize that the derivative of the graph would of a degree one less than the original graph. They carefully considered the key points of the original graph (e.g. turning points) and used these clues to plot where the corresponding values would be on the graph of the derivative. As they worked through this, it was clear to me that they were developing a solid understanding of the connections between the graph and its derivative: I am not sure this understanding would have the same clarity if they were to jump into deriving through first principles. The next day they consolidated their learning and their teacher, Leanne Oliver, sent me these photos:

The upshot of all of this is that these three components of creating a thinking classroom are having a real impact on students' learning: 

• they are doing more math
• they are taking more risks
• they are developing collaborative skills
• and they are enjoying it!

Our challenge now is to make sure that all students experience the power of a thinking classroom.

Creating Thinking Classrooms (2)

Following on from my previous post, I want to gauge the impact of three of the optimal practices highlighted by Peter Liljedahl's research into creating thinking classrooms:

• start with good questions
• use vertical non-permanent surfaces
• use visible random groups of three

I went into three classes (a Grade 4, a Grade 5, and a Grade 6) and gave the students a variant of the Precious Pentominoes activity. 

The Grade 4s were asked to use two pentominoes to create a symmetrical shape with the largest perimeter:

                 

The Grade 5s were asked to use two pentominoes to create a symmetrical shape and then calculate its cost by working out perimeter multiplied by number of sides. They then had to find the most expensive design:

The Grade 6s were asked to do the standard Precious Pentominoes task and find the most expensive design:

Look carefully and you will notice three different methods that the students have chosen for multiplying!

In terms of the three practices outlined at the start, here is what I noticed:

1) The question (which I gave orally) engaged the students from the get go. Allowing the students to use pentominoes meant that the students had multiple entry points into the problem. And the problem itself allowed the students to use many (if not all) of the Mathematical Processes. In other words, it allowed them to think mathematically.

2) The VNPSs made it much easier for me to see what each group of students was thinking. Occasionally, I noticed that some students were not measuring the perimeter carefully (showing misconceptions highlighted in this post). I was able to quickly address these misconceptions by getting the students to focus on the line segments and not the squares. 

The VNPSs also meant that students felt that students felt more comfortable showing their work in the knowledge that if they made a mistake, then they could erase it. And having the students thinking on their feet (literally!) resulted in great discussion and problem solving: more so than I have seen when students are sat down.

3) The students had no trouble at all working in the random groups. The fact that they were in groups of three meant that I had a manageable number of groups to monitor and also allowed for a good exchange of ideas between the trio. Even students who teachers identified as having difficulties with Math rose to the challenge of the problem. From what I could see, every student made some contribution.

Each of these three practices certainly had an impact in creating a thinking classroom in each of these junior grades (like it did with the intermediate class in my last post). I left each of these classes amazed by the wonderful mathematicians I had just worked with.

Now, how would it look with high school students?