- start with good questions
- use vertical non-permanent surfaces
- use visible random groups of three
I went into three classes (a Grade 4, a Grade 5, and a Grade 6) and gave the students a variant of the Precious Pentominoes activity.
The Grade 4s were asked to use two pentominoes to create a symmetrical shape with the largest perimeter:
The Grade 5s were asked to use two pentominoes to create a symmetrical shape and then calculate its cost by working out perimeter multiplied by number of sides. They then had to find the most expensive design:
The Grade 6s were asked to do the standard Precious Pentominoes task and find the most expensive design:
Look carefully and you will notice three different methods that the students have chosen for multiplying!
In terms of the three practices outlined at the start, here is what I noticed:
1) The question (which I gave orally) engaged the students from the get go. Allowing the students to use pentominoes meant that the students had multiple entry points into the problem. And the problem itself allowed the students to use many (if not all) of the Mathematical Processes. In other words, it allowed them to think mathematically.
2) The VNPSs made it much easier for me to see what each group of students was thinking. Occasionally, I noticed that some students were not measuring the perimeter carefully (showing misconceptions highlighted in this post). I was able to quickly address these misconceptions by getting the students to focus on the line segments and not the squares.
The VNPSs also meant that students felt that students felt more comfortable showing their work in the knowledge that if they made a mistake, then they could erase it. And having the students thinking on their feet (literally!) resulted in great discussion and problem solving: more so than I have seen when students are sat down.
3) The students had no trouble at all working in the random groups. The fact that they were in groups of three meant that I had a manageable number of groups to monitor and also allowed for a good exchange of ideas between the trio. Even students who teachers identified as having difficulties with Math rose to the challenge of the problem. From what I could see, every student made some contribution.
Each of these three practices certainly had an impact in creating a thinking classroom in each of these junior grades (like it did with the intermediate class in my last post). I left each of these classes amazed by the wonderful mathematicians I had just worked with.
Now, how would it look with high school students?



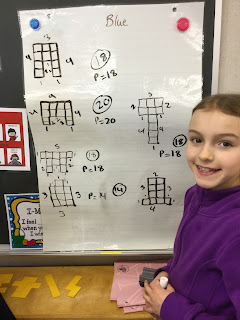









No comments:
Post a Comment