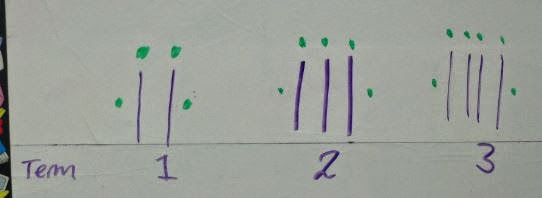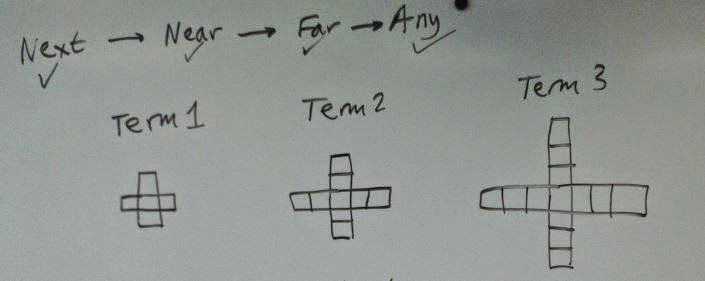"A Maths lesson without the opportunity to generalise is not a Maths lesson."
I love this quote from John Mason as it gets to the heart of what it means to think mathematically. Math is the study of patterns and the power of patterns is that they are predictable. Part of predicting a pattern is generalising a rule which we think we might have spotted. Now this is easier said than done, but doable it is providing we give students opportunities for them to generalise.
Last year, the Ontario Ministry of Education published Paying Attention to Algebraic Reasoning. When I did a word cloud of the text, it was neat to see that the word 'Generalizations' was very prominent.
For me, the biggest learning that I got from this document though was a continuum that has helped me guide students as they learn to generalise:
Next----Near----Far----Any
So I was in a Grade 6 class recently and gave them this pattern to consider:
I wondered if they could tell me how many sticks and/or dots there would be for any term. They had no trouble giving me the next term and a near term:
At this point, they were pretty clear about describing how to find the number of sticks and noticed that you just add two to this number to get the number of dots. What wasn't clear is what you do to the term number to get the number of dots (i.e. add 3). So I then pushed them to think about the thousandth term:
Note how this couldn't be drawn out but they got the 1001 sticks straight away and soon had also told me that 1003 dots were needed. Had they made the link between the term number and the number of dots? I decided to really push the envelope and asked them to generalise for any (i.e. the nth) term. Straight away they said the number of sticks would be n+1 but they needed a bit more help with the number of dots being n+3. Still, not so bad as it was the start of the unit and with further exposure.
Now I was unsure if it was helpful just drawing the pattern on the board: is it better for students to have the pattern modelled with manipulatives at their desk? I was in another class, a split Grade 6/Grade 7 and we gave each student a set of three cubes that were linked together. We asked the students to put them on the desk and tell us how many square faces they could see. When we all agreed that it was 11 we then asked the Grade 6s to find out how many square faces are visible on a set of 10 cubes (near) and the Grade 7s a set of 50 cubes (far). Notice how we skipped the 'next' stage here. Very quickly they were able to use the cubes to help explain their thinking:
The Grade 6s then tried the Grade 7 question whilst the Grade 7s were asked to make an 'any' prediction. We got three possible answers for this:
n+n+n+2
(n×3)+2
3n+2
(Note: In both these cases, I basically gave the student the patterns but would not always do this: it is vital that students create and test their own patterns.)It was interesting to see, as my colleague Christine pointed out, that the students who said the first answer may be thinking more additively than the multiplicative thinking of the other two answers. With more experience of these types of tasks, students will develop the skills that are needed to generalise.
(Update to original post):
I spent another lesson with the same class and actually showed them the next-near-far-any continuum. I challenged them to see how far along the continuum they could go for this pattern:
It was great to see that so many students are already using their spatial reasoning to help the generalising as best exemplified by this:
 * * *
* * *The Ontario MOE's Paying Attention to Algebraic Reasoning can be found here.