Joyous Maths: Dan's Favourite Pattern

The wonderful James Tanton speaks of the importance of getting our students (indeed everyone) to experience 'joyous maths'. One of the most satisfying sounds for any teacher is the squeal of delight and the "Oh, that is so neat!" when a problem has been solved. My colleague Dan Allen (past-president of OMCA) recently confessed that this is his favourite visual pattern.

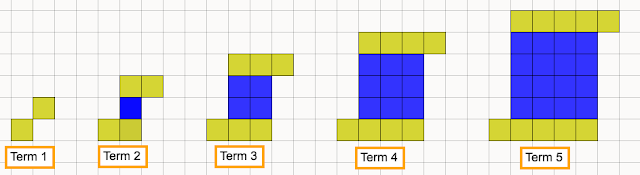
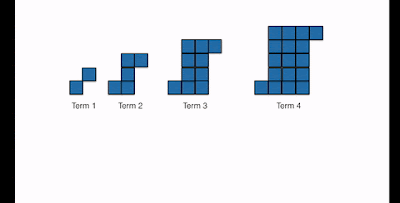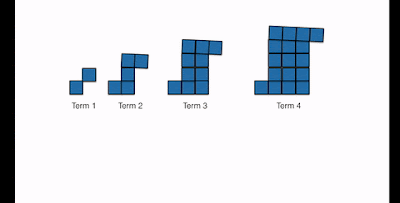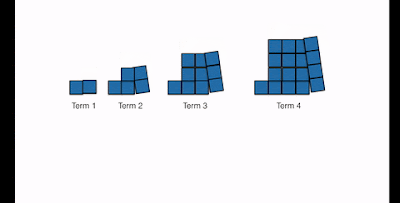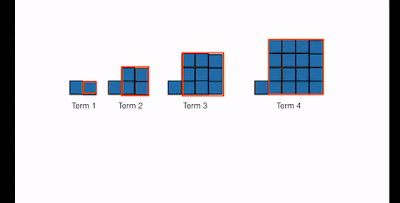
A typical question to accompany a question like this might be 'How many squares are in the hundredth term?' or even 'what is the nth term?' In the past, I have dutifully created a table of values and used all sorts of algebraic techniques to come up with such an algebraic rule. This is fine, to an extent, but if this is all we do (or get our students to do) then we are missing out on a grand opportunity to do some beautiful maths.
So why does Dan get so excited about this pattern? Think about how many different ways it can be seen:

Perhaps you see it as an inner rectangle and two squares. Generalising this suggests an nth term of (n-1)(n+1)+2 

Maybe you see an inner square and two identical rectangles. Generalising, this suggests an nth term of (n-1)2+2n

Maybe you see an opportunity to complete an 'outer' square with two identical rectangles. Generalising, this suggests an nth term of (n+1)2– 2n

Or maybe you transformed the pattern by taking the top layer of each term, rotating it 90˚ to create a large square and a small square. 

Generalising, this suggests an nth term of n2+1.

In fact, much fun can be had showing that all these general terms do simplify to n2+1.

Visual patterns like these are so important as they allow us to be able to decompose shapes in different ways. This in turn helps us generalise by moving along the Next, Near, Far, Any continuum. Indeed, I am noticing how effective it is to get students (and adults) to generalise by asking them to 'draw' the hundredth term. When I did so recently in  Grade 9 class, the students moved on from drawing individual tiles to thinking about the dimensions of the inner rectangle and thence how to write this algebraically:

So I set myself a challenge: create a new visual pattern that will become Dan's new favourite puzzle. This in itself involved much problem solving and eventually I came up with this:

Using decomposing strategies like those shown above, how can we describe the hundredth term? the nth term? How many ways can we see this?

I showed it to Dan. He liked it (how much I'm not sure) and funnily enough, he saw it in a different way than I. He then set about creating a 'decomposable' visual pattern of his own:

So, be honest, which of these is the most joyous?

*          *          *

These diagrams were created using the Colour Tiles from the  mathies.ca site.