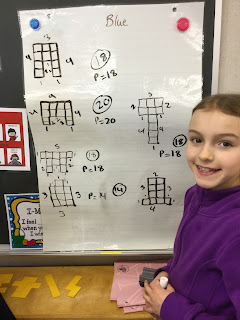Creating Thinking Classrooms (3)

Having done some work on creating a thinking classroom with junior and intermediate students (see my last two posts), I was keen to see how high school students would react. Again, I wanted to gauge the impact of three of the optimal practices for creating a thinking classroom as outlined by Peter Liljedahl:

• start with good questions
• use vertical non-permanent surfaces
• use visible random groups of three

The first problem I tried this with was actually one Peter Liljedahl had shared with us at the Ontario Mathematics Coordinators Association's conference.
Using the numbers 1 to 10, and the operations +, –, ✕, ÷ plus another one of these operations, create five number sentences that have the following solutions:

17     2     21     3      2

(For what it is worth, this question is a lot easier to understand when the instructions are given orally!)

The students got stuck into this problem immediately. Being free to move around the room I was able to listen to some impressive number sense and logic. I'd go so far as to say that the students were more accomplished at this than adults who I have given the task to.

When they solved it, I gave another set of answers:
2    2    2    2    9
and later
10   14   1   20   16

 Next, I gave one of the Problems of the Week from our @DCDSBMath twitter feed:

As students quickly solved this, I then asked them to consider a 10-by-10 array with the top square missing and, from there, to consider the general case:

 Many groups looked at of squares of different sizes and noticed that these were one less than a perfect square. It was a nice opportunity for me to introduce sigma notation:

One group gave me math bumps though as they saw the number of squares of different sizes in a different way which connected beautifully to the difference of squares:

Perhaps the strongest feeling I take away from this is the amount of math that the students are doing. They are not sitting passively copying a note, they are actually being mathematicians.
It is something I have seen before in a Grade 9 class (this post) and I also saw recently in a Grade 12 calculus class. Students were asked to sketch a graph of any function they wanted and to then use what they know of the derivative to sketch the graph of the derivative (without resorting to deriving by first principles). Students were first sorted visibly into random groups by being given a card and then having to find the corresponding representations:

They then got stuck into the task:

 and as they did so, they began to challenge themselves more:

Remember, the students had to choose their own graphs for this activity. The discussions that took place were a joy to behold. Independently, they began to hypothesize that the derivative of the graph would of a degree one less than the original graph. They carefully considered the key points of the original graph (e.g. turning points) and used these clues to plot where the corresponding values would be on the graph of the derivative. As they worked through this, it was clear to me that they were developing a solid understanding of the connections between the graph and its derivative: I am not sure this understanding would have the same clarity if they were to jump into deriving through first principles. The next day they consolidated their learning and their teacher, Leanne Oliver, sent me these photos:

The upshot of all of this is that these three components of creating a thinking classroom are having a real impact on students' learning: 

• they are doing more math
• they are taking more risks
• they are developing collaborative skills
• and they are enjoying it!

Our challenge now is to make sure that all students experience the power of a thinking classroom.

Creating Thinking Classrooms (2)

Following on from my previous post, I want to gauge the impact of three of the optimal practices highlighted by Peter Liljedahl's research into creating thinking classrooms:

• start with good questions
• use vertical non-permanent surfaces
• use visible random groups of three

I went into three classes (a Grade 4, a Grade 5, and a Grade 6) and gave the students a variant of the Precious Pentominoes activity. 

The Grade 4s were asked to use two pentominoes to create a symmetrical shape with the largest perimeter:

                 

The Grade 5s were asked to use two pentominoes to create a symmetrical shape and then calculate its cost by working out perimeter multiplied by number of sides. They then had to find the most expensive design:

The Grade 6s were asked to do the standard Precious Pentominoes task and find the most expensive design:

Look carefully and you will notice three different methods that the students have chosen for multiplying!

In terms of the three practices outlined at the start, here is what I noticed:

1) The question (which I gave orally) engaged the students from the get go. Allowing the students to use pentominoes meant that the students had multiple entry points into the problem. And the problem itself allowed the students to use many (if not all) of the Mathematical Processes. In other words, it allowed them to think mathematically.

2) The VNPSs made it much easier for me to see what each group of students was thinking. Occasionally, I noticed that some students were not measuring the perimeter carefully (showing misconceptions highlighted in this post). I was able to quickly address these misconceptions by getting the students to focus on the line segments and not the squares. 

The VNPSs also meant that students felt that students felt more comfortable showing their work in the knowledge that if they made a mistake, then they could erase it. And having the students thinking on their feet (literally!) resulted in great discussion and problem solving: more so than I have seen when students are sat down.

3) The students had no trouble at all working in the random groups. The fact that they were in groups of three meant that I had a manageable number of groups to monitor and also allowed for a good exchange of ideas between the trio. Even students who teachers identified as having difficulties with Math rose to the challenge of the problem. From what I could see, every student made some contribution.

Each of these three practices certainly had an impact in creating a thinking classroom in each of these junior grades (like it did with the intermediate class in my last post). I left each of these classes amazed by the wonderful mathematicians I had just worked with.

Now, how would it look with high school students?