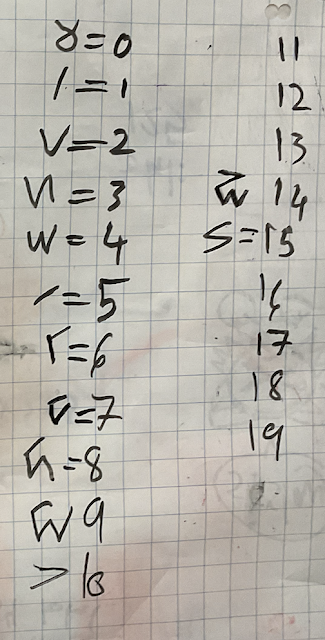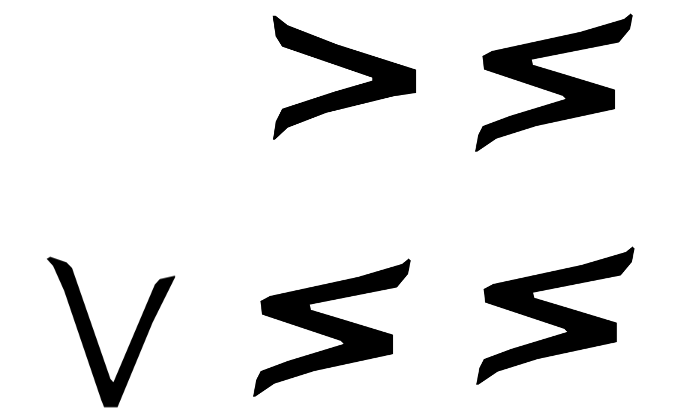Quadratic Card Sort

My grade 10s have been working on quadratic relations and I thought that a good way to help them consolidate all their learning was to give them this card sort. I first saw this years ago in the NCETM's Improving Learning in Mathematics and I made some slight adaptations.

I started by giving the students these two sets of cards:

and they began cutting them out and matching the standard form to the factored form:

Immediately, there were lots of great discussions on factoring, too many almost to track!

When I saw that a group had made the correct matches, I then gave them these cards about the intercepts:

I had debated about whether I should label these with 'x-intercepts' and 'y-intercept' but then thought it would be better for the students to figure out this themselves (which they did!)

When these matches were made, I then gave them the seven graphs (created with the help of Desmos)

Lots of good connections were being made now as students used the factored form and the intercepts to make their decisions. They were then ready for the next set of cards which were the maxima or minima.

These were matched quickly: the graphs helped a lot but I was able to get students to check that each vertex lay halfway between the x-intercepts.

Finally, I gave the cards with the vertex form:

I have not done vertex form with them yet so I was curious as to how they would manage with these. But by using a bit of intuition, they matched the y=(x–5)^2–9 equation with the card that said 'Minimum: (5, -9)' I could then ask groups to expand and simplify the vertex form to see that it matched the standard form of y=x^2+10x+16.

As they beagan to match some of the other vertex form graphs, I could hear some groups making conjectures along the lines of 'Look at the co-ordinates of the vertex, make the x one opposite of what it is but keep the y one the same and then look for that equation.' In doing so, most groups came up with a full set as shown: 

At this point, I was able to get the class to see that when we write an equation in vertex form, it allows us to immediately see the co-ordinates of the vertex which, for some problem solving situations, is important to know. They will learn more about this in the next unit.

Finally, each set of cards purposely had a blank template so I challenged the students to create their own set of cards. I wish I left more time for this though as most groups did not have enough time to complete a full set of cards (a sample is shown below):

If you would like to try this yourself, the cards can be found here.

Kaktovik Numerals

 In August 2021, I stumbled across the wonderful Katovik numeral system.

Kaktovik is a city in northern Alaska. In the 1990s, the students at a school in Kaktovik realised that there were problems matching Hindu-Arabic numerals to the patterns of their Iñupiaq language. As part of their math enrichment class, they set out to create new numerals that matched their language.

The Iñupiaq language of Alaska uses a Base-20 for its numerals with subdivisions for groups of 5. There are some rule breakers (looking at you, 6) and numbers before a multiple of 5 have a subtractive element '-utaiḷaq' included so 14 is a bit like saying 15 – 1.

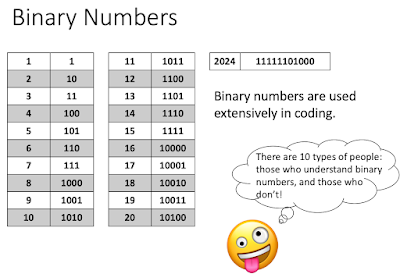
The students devised a brilliant numeral system that matched their language (revealed below). I created and shared a task that teachers could use to get their students to learn about these wonderful numerals. This was originally meant to be a task for Grade 9s but today I tried it with two Grade 8 classes for the first time.

First, I showed them that they are already familiar withe different number systems that we use:

I told the students the story of how the students in Kaktovik wanted to create numerals that matched their language (as shown above) and then (after splitting the students into visibly random groups) I gave them the following clues and challenged them to find all twenty Kaktovik numerals:

Immediately, all groups got stuck into the task. The first two clues were quickly deciphered to give the symbols for 1 and 2. These allow us to make sense of the third clue to find the symbol for 3 which can then be used in the fourth clue to find the symbol for 5. The next clue (which represents 4 + 4) helps us to get the symbol for 8:

At this point, I did remind some groups that there was a pattern behind the symbols that matched the Iñupiaq language. Once they understood that the symbols were not random, they began to make sense of the pattern to complete the numerals to ten. The sixth and seventh clues helped them fill in some other values for 14 and 15:

The penultimate clue was quickly deciphered by most groups to get the symbol for 0 which then allowed them to make sense of the last clue: 10 times by 2 equals 20. Using Kaktovik numerals, this is written as one group of twenty and zero ones. There was a lot of excitement in the room as students completed their work:

I then showed them how the place value columns in Base 20 differ to those in Base 10 i.e. to the left of the ones column, we have the twenties column and to the left of that we have the 20 squared (or four hundreds) column. I then challenged them to rewrite this Kaktovik numerals: 

This was definitely a challenge for some groups but I was pleased to see a lot of success with this.

Finally, I put up some 'Mild, Medium and Spicy' questions for them to try: 

This worked really well as students self-differentiated and all felt that they rose to the challenge:

There is now a Kaktovik numerals calculator app and I was able to show this to the students to check any given calculation. They really enjoyed seeing this!

I finished the lesson by making three important points:

• There are pros and cons to any numeral system.
• Don't assume that what you are familiar with is always the best way of doing things.
• Anyone can create math that can have a positive impact on their community.

*            *            *

More information about the development of Kaktovik numerals and how they can be used to facilitate arithmetic operations can be found in this Scientific American article from April 2023.

UPDATE:

Some colleagues tried this in another Grade 8 class and saw this on one group's work!